Мій сайт

Формула трапецій численного інтегрування функцій.

Задача состоит в нахождении приближенного значения интеграла.

 

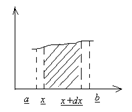
b                                                        

  ∫f(x)dx – сумма елементарных площадей, ограниченых снизу

a             отрезком   x; x+dx, сверху – линией функции F(x) и

                  ординатами в точках x и x+dx. Интеграл – это

                  функция F(x), произвлдная которой F(x) = f(x) + e

                   b

                   ∫f(x)dx = F(b) – F(a)

                a

Суть метода трапеций:

 

Дано:      1) F(x)                                                                                                                 b

  2) [a;b] – для которых требуется найти значения интеграла   I = ∫f(x)dx

                                                                                                           a

   Приближенное значение интеграла находим как сумму площадей

           n

   I = ∑ S _i            S _i = (       n       )           Y₁ + Y_i+1     где  Y_i = F(x_i)

            i = 1                    x_i+1 – x₁                         2

если все интервалы взять равными, то можно получить формулу:

  I = h/2 (Y₀ +2Y₁ +2Y₂ + ... + Y_n )

                                  n - 1

  I = h/2 ( Y₀ + Y_n + 2 ∑ Y₁ ) -  формула трапеции.

                                  i = 1

Чем меньше границы интервалов, тем больше точность.